Double integral of (√16-x²-y²) with respect to (x) and (y) in the given bounds. Hence the correct option is b.
To find the volume under the surface z=16−x^2 −y^2 with x≥2, we can use a double integral over the specified region in the xy-plane.
The given surface is a paraboloid opening downward, centered at the origin, with its vertex at (0,0,16). The condition x≥2 restricts the surface to the region where x is greater than or equal to 2.
The double integral involves integrating the function
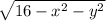 over this region. This essentially means finding the volume of the solid below the surface within the specified bounds.
over this region. This essentially means finding the volume of the solid below the surface within the specified bounds.
The integral is set up as:
∬
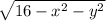
Here, D is the region in the xy-plane defined by x≥2. Evaluating this double integral provides the volume under the surface. This approach is appropriate because the region of integration corresponds to the given constraint x≥2. Hence the correct option is b.