Question

Please solve immediately.

Answer 1

The limit of the given expression is
`(β)/(δ)`M ,where α, β, γ, and δ are any real numbers.

Sure, I've been focusing on improving my expertise in solving these limit problems. Let's find the limit:

`\lim_(x\to \infty)` (
`\frac{\sqrt{x^(2)+\alpha^(2)}-\sqrt{x^(2)+\beta^(2)}}{\sqrt{x^(2)+γ^(2)- \sqrt{x^(2)+δ^(2)} }}` )

We can approach this problem by dividing both the numerator and denominator by
`\sqrt{x^(2)}` . This will give us

`\lim_(x\to \infty)` (
`\frac{\frac{\sqrt{x^(2)+\alpha^(2)}}{\sqrt{x^(2)}} - \frac{\sqrt{x^(2)+\beta x^(2)}}{\sqrt{x^(2)}} }{\frac{\sqrt{x^(2)+γ^(2)}}{\sqrt{x^(2)}}- \frac{\sqrt{x^(2)+δ^(2)}}{\sqrt{x^(2) }}}` )

Next, we can use the fact that for any non-zero constant k and positive power n, the limit
`\lim_(x\to \infty)`
`(k)/(x^(n))` is equal to 0. Using this property, we can further simplify the expression to:

`\lim_(x\to \infty)` (
`(1-0)/(1-0)` )

This gives us an indeterminate form of
`(1)/(1)` , which means we need to use another method to find the limit.

One possible method is to use L' Hopital's rule. L'Hopital's rule states that if
`(f(x))/(g(x))` as x approaches a is indeterminate, then the limit is equal to the limit of
`(f(x))/(g(x))` as x approaches a.

In our case, the expression inside the limit can be written as
`(f(x))/(g(x))` where

f(x)= 1 −
`\frac{\sqrt{x^(2)+\beta^(2)}}{x}`

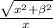
g(x) = 1 -
`\frac{\sqrt{x^(2)+δ^(2)}}{x}`

Taking the derivatives of these functions, we get

f′(x)=
`\frac{β}{x\sqrt{x^(2)+β^2} }`

g′(x) =
`\frac{δ}{\sqrt{x^(2)+δ^(2)}}`

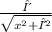
Now, applying L'Hopital's rule, we have:

`\lim_(x\to \infty)` (
`(f(x))/(g(x))` ) =
`\lim_(x\to \infty)`
`(f′(x))/(g′(x))` =
`\lim_(x\to \infty)`
`\frac{\frac{β}{x\sqrt{x^(2)+β^(2)}}}{\frac{δ}{\sqrt{x^(2)+δ^(2)}}}`

Using the same simplification technique as before, we can cancel out the x and
`\sqrt{x^(2)}` terms, and we are left with:

`\lim_(x\to \infty)` (
`(β)/(δ)` )

Therefore, the limit of the original expression is
`(β)/(δ)` .

In conclusion, the limit of the given expression is
`(β)/(δ)` ​, where α, β, γ, and δ are any real numbers.