The length of BD is 4/3 cm
The diagram shows a right triangle ABC, with DE parallel to BC. We are asked to find the length of BD, given that the base of the triangle is 2 cm and the height is 1 cm.
Since DE is parallel to BC, we know that triangle ADE is similar to triangle ABC. We can use the following ratio to find BD:
BD/BC = AD/AC
We are given that BC = 2 cm and the height of the triangle (AC) is 1 cm. We can find AD using the Pythagorean theorem:
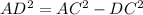
where DC = BC - BD (since BD + DC = BC)
Substituting the known values, we get:
 =
=
 -
-
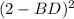
Simplifying the equation, we get:
 = 1 - (4 - 4BD +
= 1 - (4 - 4BD +
 )
)
 = 4BD - 3
= 4BD - 3
Taking the square root of both sides, we get:
AD = 2√(BD) - √3
Now we can substitute this value of AD in the ratio:
BD/BC = AD/AC
BD/2 = (2√(BD) - √3) / 1
Simplifying the equation, we get:
BD = 4√(BD) - 2√3
Solving for BD, we get:
3√(BD) = 2√3
Squaring both sides, we get:
9BD = 12
BD = 4/3 cm
Therefore, the length of BD is 4/3 cm.
The probable question may be:
"In the given figure find BD, if DE ll Bc"