The orthocenter of the triangle formed by (0,0), (4,3), and (3,6) is at (0,0) because the perpendiculars from each vertex intersect there. Therefore, the answer is option D.
Given the points (0,0), (4,3), and (3,6), let's proceed with the calculations.
Slope of the line passing through (0,0) and (4,3):
![\[ \text{Slope} = \frac{{3 - 0}}{{4 - 0}} = (3)/(4) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/yfd0216gwzi4woefi1bxxsn98igi3q6myz.png)
Slope of the line passing through (0,0) and (3,6):
![\[ \text{Slope} = \frac{{6 - 0}}{{3 - 0}} = 2 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/2pc9f03yipm6z5glibekixdl1ul3s92kiy.png)
Now, the negative reciprocal of these slopes will give us the slopes of the perpendicular lines passing through each pair of points.
For the line passing through (0,0):
Slope of the perpendicular line to (0,0) and (4,3) :
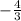
Slope of the perpendicular line to (0,0) and (3,6):
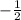
Using the point-slope form (y - y1 = m(x - x1)) with the slopes and respective points, we get the equations of the perpendicular lines:
Equation of the line passing through (0,0) and having a slope of
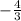
![\[ y - 0 = -(4)/(3)(x - 0) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/yk2mibtdc5wa0o8mjd2knxy1g5z3w20uqd.png)
![\[ y = -(4)/(3)x \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/7z84om6d5chw10p50oba0jabdwldmyo6qk.png)
Equation of the line passing through (0,0) and having a slope of
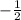 :
:
![\[ y - 0 = -(1)/(2)(x - 0) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/k5hwcs39cl06ccwj08zn393btx32db4t8y.png)
![\[ y = -(1)/(2)x \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/rpnd86utyqre3i1kirxaaznc9hru0g2da6.png)
Now, to find the intersection point (which is the orthocenter), solve these two equations simultaneously:
![\[\begin{cases} y = -(4)/(3)x \\y = -(1)/(2)x \end{cases}\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/83ozq2aqwtsedhx35orbsf1j7930vdfumj.png)
Setting the equations equal to each other:
![\[ -(4)/(3)x = -(1)/(2)x \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/aeqy7gq890xrhyu0z4jfzzyye6j2vd7bwt.png)
![\[ -4x = -(3)/(2)x \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/6veneead90wp2prsn5m5pum8xjsbzoj0tm.png)
![\[ x = 0 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/kifoh5xx9lghwlgy0l92uqw2p6vugj1nar.png)
Plugging
 into either equation:
into either equation:
![\[ y = -(1)/(2)(0) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/ig2xzol8gswfklfjvf4jk80adbt93b03ly.png)
![\[ y = 0 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/qii7laa3rret6s177ci802hvmio9ngaxgt.png)
Therefore, the orthocenter of the triangle formed by the points (0,0), (4,3), and (3,6) is at the point (0,0), which matches option D.
complete the question
The orthocenter of the triangle formed by the points (0,0), (4,3), and (3,6) is located at:
A) (2, 1)
B) (3, 2)
C) (1, 3)
D) (0, 0)
E) None of the above