Question

For the given equation, find the values of a, b, and c, determine the direction in which the parabola opens, and determine the y-intercept:

y = negative 4 x squared

Answer 1

The equation
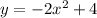`\(y = -2x^2 + 4\)` has a downward-opening parabola (due to
`(\(a = -2\))`. Its y-intercept is at (0, 4). A table with (0, 4) best illustrates these values.

Given equation:
`\(y = -2x^2 + 4\)`

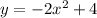
Determine Values of \(a\), \(b\), and \(c\) in the Quadratic Equation Form
`\(y = ax^2 + bx + c\)`

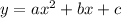
For the given equation,
`\(a = -2\)` (coefficient of
`(\(x^2\))`,
`\(b = 0\)` (since there is no
`(\(x\) term)` , and
`\(c = 4\)`

Determine the Direction in Which the Parabola Opens:

Since
`\(a = -2 < 0\)`, the parabola opens downward.

Find the Y-intercept:

To find the y-intercept, substitute
`\(x = 0\)` into the equation:

`\[y = -2(0)^2 + 4 = 4\]`

The y-intercept is 4, and it occurs at the point (0, 4).

Table Representation:

The best table to illustrate these values would include:

|
`\(x\)` |
`\(y\)` |

| 0 | 4 |

This table shows the y-intercept where
`\(x = 0\)`and the corresponding \(y\) value of 4. There's no linear term
`(\(bx\))`, so the \(b\) value doesn't affect the table, remaining as 0 in this case.

Therefore, for the equation
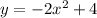`\(y = -2x^2 + 4\)`, the parabola opens downward, the y-intercept is 4 at (0, 4), and the table best illustrating these values includes the point (0, 4).