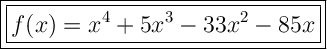Question

Write a polynomial function f of least degree that has a leading coefficient of 1 and the given zeros. Write the function in standard form.

0,5,−5+√8
PLS help :(

Answer 1

`f(x)=x^4+5x^3-33x^2-85x`

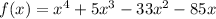
Explanation:

The complex conjugate root theorem states that if a polynomial with real coefficients has a complex root (a + bi), then its conjugate (a - bi) is also a root of the polynomial.

Therefore, given that (-5 + √8) is a complex root of function f, then (-5 + √8) is also a root.

The factored form of a polynomial with zeros r₁, r₂, ... rₙ and leading coefficient "a" is given by:

`f(x)=a(x-r_1)(x-r_)...(x-r_n)`

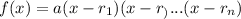
In this case, the zeros are:

• 0
• 5
• (-5 + √8)
• (-5 - √8)

Given that the leading coefficient is 1, then factored form of the polynomial is:

`f(x)=(x-0)(x-5)(x-(-5+√(8)))(x-(-5-√(8)))`

Simplify:

`f(x)=x(x-5)(x+5-√(8))(x+5+√(8))`

`f(x)=x(x-5)(x^2+5x+√(8)x+5x+25+5√(8)-√(8)x-5√(8)-8)`

`f(x)=x(x-5)(x^2+5x+5x+√(8)x-√(8)x+5√(8)-5√(8)+25-8)`

`f(x)=x(x-5)(x^2+10x+17)`

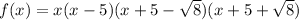
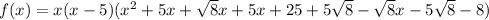
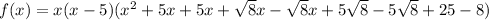
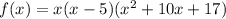
To write the function in standard form, expand the brackets:

`f(x)=(x^2-5x)(x^2+10x+17)`

`f(x)=x^4+10x^3+17x^2-5x^3-50x^2-85x`

`f(x)=x^4+5x^3-33x^2-85x`

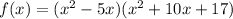
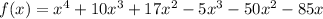
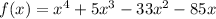
So, the polynomial function f of least degree that has a leading coefficient of 1 and the zeros 0, 5, and (-5 + √8) in standard form is:

`\Large\boxed{\boxed{f(x)=x^4+5x^3-33x^2-85x}}`