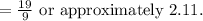=
=
 or approximately 2.11.
or approximately 2.11.
To solve the expression
 let's start by converting the mixed numbers to improper fractions.
let's start by converting the mixed numbers to improper fractions.
 can be written as
can be written as
 because
because
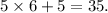
Similarly,
 can be expressed as
can be expressed as
 because
because
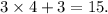
Now, the expression becomes

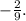
To divide fractions, multiply by the reciprocal of the divisor, so we get
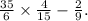
Simplify the fractions:
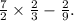
Multiply the numerators and denominators separately:
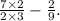
This results in

Find a common denominator, which is 18:

This simplifies to
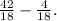
Now, subtract the numerators:
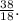
Finally, simplify the fraction by dividing both the numerator and denominator by their greatest common factor, which is 2:
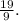
So,