Question

if a certain sum of money amounts to ₹27960 in 3years and amounts to ₹34560 in 8 years at the same rate of si, find the sum and the rate of interest applicable.​

Answer 1

The principal sum is approximately ₹2,796,610.17, and the rate of interest is approximately 4.72%. These values satisfy the given conditions of simple interest over 3 and 8 years.

To find the principal sum and the rate of interest, we can use the formula for simple interest:

`\[ A = P \left(1 + (rt)/(100)\right) \]`

Where:

- A is the amount after t years,

- P is the principal sum (initial amount),

- r is the rate of interest, and

- t is the time in years.

Given that A = ₹27960 after 3 years and A = ₹34560 after 8 years, we can set up two equations:

For 3 years:

`\[ 27960 = P \left(1 + (3r)/(100)\right) \]`

For 8 years:

`\[ 34560 = P \left(1 + (8r)/(100)\right) \]`

Now, you can solve these two equations simultaneously to find P and r. Subtract the first equation from the second to eliminate P:

`\[ 34560 - 27960 = P\left((8r)/(100) - (3r)/(100)\right) \]\[ 6600 = P \left((5r)/(100)\right) \]`

Now, solve for P:

`\[ P = (6600)/((5r)/(100)) \]\[ P = (6600 * 100)/(5r) \]\[ P = (660000)/(5r) \]\[ P = 132000 / r \]`

Now, substitute the value of P back into either of the original equations to solve for r. Once you find r, you can find P using the equation
`\( P = (660000)/(5r) \).`

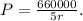
Now, substitute this expression into one of the original equations, for example, the equation for 3 years:

`\[ 27960 = (132000)/(r) \left(1 + (3r)/(100)\right) \]`

Now, solve for r:

`\[ 27960 = (132000)/(r) + (3960)/(100) \]`

Combine the fractions:

`\[ 27960 = (132000)/(r) + 39.6 \]`

To simplify, let's multiply through by r to clear the fraction:

`\[ 27960r = 132000 + 39.6r \]`

Subtract 39.6r from both sides:

`\[ 27960r - 39.6r = 132000 \]`

Combine like terms:

`\[ 27920.4r = 132000 \]`

Now, solve for r:

`\[ r = (132000)/(27920.4) \]\[ r \approx 4.72\% \]`

Now that we have the rate of interest r, you can substitute it back into the expression for P to find the principal amount P:

`\[ P = (132000)/(4.72\%) \]\[ P \approx 2,796,610.17 \]`

Therefore, the principal sum is approximately ₹2,796,610.17 and the rate of interest is approximately 4.72%.