Setting the equations equal:
 After solving,
After solving,
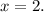 Substituting into either equation gives \(y = -5\). The point of intersection is
Substituting into either equation gives \(y = -5\). The point of intersection is
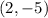 .
.
To solve for the point of intersection between the lines
 and
and
 , we'll equate the two equations and solve for
, we'll equate the two equations and solve for
 :
:
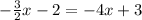
First, let's eliminate the fractions by multiplying all terms by 2 to get rid of the denominator:
let's gather the
 terms on one side by adding
terms on one side by adding
 to both sides:
to both sides:
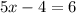
Now, isolate the
 term by adding 4 to both sides:
term by adding 4 to both sides:
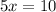
Finally, solve for
 by dividing both sides by 5:
by dividing both sides by 5:

Now that we have
 let's find the corresponding \(y\) value using one of the original equations. We'll use
let's find the corresponding \(y\) value using one of the original equations. We'll use
 :
:
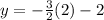
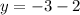

Therefore, the point of intersection occurs at
 and
and
 which gives us the coordinates of the intersection point as
which gives us the coordinates of the intersection point as
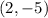 .
.
complete the question
"Two lines,
 and
and
 , intersect at a point. What are the coordinates of this point of intersection? Illustrate your answer graphically to show how you arrived at the solution."
, intersect at a point. What are the coordinates of this point of intersection? Illustrate your answer graphically to show how you arrived at the solution."