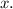Final Answer:
(c)

Step-by-step explanation:
To find the inverse of
 , interchange
, interchange
 and
and
 and solve for the new
and solve for the new
 . Start with the original equation:
. Start with the original equation:
![\[ x = (1)/(5)e^y + 2 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/rk2cl8qr18jww62m9ipxr3yk9jxmqby2c0.png)
Subtract 2 from both sides:
![\[ x - 2 = (1)/(5)e^y \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/y96v86zb6gqfnzb259qtzqvi0npl2o0dkh.png)
Multiply both sides by 5 to isolate
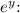
![\[ 5(x - 2) = e^y \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/rhs9cyp72kdedjk761kujrun5yyei4k1zn.png)
Now, take the natural logarithm (ln) of both sides to solve for
 :
:
![\[ y = \ln(5x - 10) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/5e3ulie79m7hxy9cojrjh1lemtuwbhpzj9.png)
Simplify further by expressing
 as
as
 :
:
![\[ y = \ln(5x - 10) = \ln(5(x - 2)) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/quqflg1jkg7zvdc9e0ts8utqw4h3daxlfz.png)
Thus, the equation of the inverse function is
 , corresponding to option (c).
, corresponding to option (c).
Understanding the process of finding the inverse function is crucial in solving mathematical problems involving functions. The key steps involve swapping
 and
and
 , isolating
, isolating
 and expressing the inverse function in terms of
and expressing the inverse function in terms of