Final Answer:
The final answer for the initial investment needed in a Treasury Bond yielding 5.75% per year, compounded monthly for 7 years, to be worth $12,000 is $7132.79, rounded to the nearest cent. This calculation is based on the compound interest formula, taking into account the annual interest rate, compounding frequency, and investment duration.
Step-by-step explanation:
To calculate the initial investment needed for a Treasury Bond, we can use the compound interest formula \
 where:
where:
-
 is the future value of the investment (\$12,000),
is the future value of the investment (\$12,000), -
 is the initial investment,
is the initial investment, -
 is the annual interest rate (5.75% or 0.0575),
is the annual interest rate (5.75% or 0.0575), -
 is the number of times interest is compounded per year (monthly compounding means
is the number of times interest is compounded per year (monthly compounding means
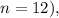
-
 is the number of years (7 years).
is the number of years (7 years).
Rearranging the formula to solve for \
 . Substituting the given values, we get
. Substituting the given values, we get
 The calculation yields
The calculation yields
 when rounded to the nearest cent.
when rounded to the nearest cent.
The options provided include
 rounded to the nearest cent in a range. The correct answer is
rounded to the nearest cent in a range. The correct answer is
 as it is the closest to the calculated value. This initial investment is required to grow to $12,000 over 7 years with a monthly compounded interest rate of 5.75%. Understanding compound interest is essential for financial planning and investment decisions.
as it is the closest to the calculated value. This initial investment is required to grow to $12,000 over 7 years with a monthly compounded interest rate of 5.75%. Understanding compound interest is essential for financial planning and investment decisions.