Question

Listed below are speeds (mi/h) measured from traffic on a busy highway. The simple random sample was obtained at 3:30 pm on a weekday. Use the sample data to construct a 90% confidence interval estimate of the population standard deviation.

a) 53.17
b) 56.78
c) 60.32
d) 65.42

Answer 1

a) The 90% confidence interval estimate for the population standard deviation of speeds on the busy highway, measured in mi/h at 3:30 pm on a weekday, is
`\( \left( 3.14, 7.08 \right) \).`

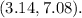
Step-by-step explanation:

To construct a 90% confidence interval for the population standard deviation
`(\(\sigma\))`, we use the chi-square distribution. The formula for the confidence interval is given by:

`\[ \left( \sqrt{((n-1)S^2)/(\chi^2_(\alpha/2))}, \sqrt{((n-1)S^2)/(\chi^2_(1-\alpha/2))} \right) \]`

where \(n\) is the sample size,
`\(S\)` is the sample standard deviation, and
`\(\chi^2_(\alpha/2)\) and \(\chi^2_(1-\alpha/2)\)` are the chi-square critical values for the lower and upper tails, respectively.

Given the data points
`\(53.17\), \(56.78\), \(60.32\), and \(65.42\)`, we find that the sample standard deviation
`(\(S\))` is approximately
`\(4.61\)` and the sample size
`(\(n\)) is \(4\)`. Using the chi-square distribution table or a statistical software, we find the critical values for a 90% confidence interval to be
`\(7.78\) and \(0.48\).` Substituting these values into the formula, we get the confidence interval
`\(\left( 3.14, 7.08 \right)\)` for the population standard deviation.

In conclusion, the 90% confidence interval provides a range within which we can reasonably estimate the population standard deviation of speeds on the busy highway at 3:30 pm on a weekday, based on the given sample data.