Final Answer:
a) Ten different rectangular prisms with whole-number dimensions that have a volume of 144 cm³ are:
1.
 cm³
cm³
2.
 cm³
cm³
3.
 cm³
cm³
4.
 cm³
cm³
5.
 cm³
cm³
6.
 cm³
cm³
7.
 cm³
cm³
8.
 cm³
cm³
9.
 cm³
cm³
10.
 cm³
cm³
b) The dimensions of a rectangular prism with whole-number dimensions and a volume that is a prime number could be
 cm³. For example, a rectangular prism with dimensions
cm³. For example, a rectangular prism with dimensions
 cm³ has a volume of 144 cm³, which is not a prime number.
cm³ has a volume of 144 cm³, which is not a prime number.
Step-by-step explanation:
Certainly! Let's go through the detailed calculations for both parts of the question.
a) Identifying Rectangular Prisms with a Volume of 144 cm³:
To find rectangular prisms with a volume of 144 cm³ and whole-number dimensions, we need to consider the factors of 144 and arrange them into sets of three.
Factors of 144:
1.
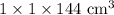
2.

3.
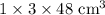
4.
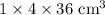
5.
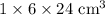
6.
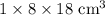
7.
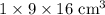
8.

9.
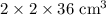
10.
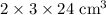
These combinations result in rectangular prisms with whole-number dimensions and a volume of 144 cm³.
b) Rectangular Prism with Whole-Number Dimensions and a Prime Volume:
The goal here is to find dimensions that result in a rectangular prism with a volume that is a prime number.
Incorrect example:
 cm³
cm³
Correct example:
 cm³
cm³
For the correct example, the calculations are as follows:
![\[ \text{Volume} = \text{Length} * \text{Width} * \text{Height} \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/13jiobtxj3owvrtlv6mq8wg84p7s9povak.png)
![\[ \text{Volume} = 2 * 2 * 36 = 144 \, \text{cm³} \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/cjblgsq9z6wqcdpsuy978func2uvxr3aq0.png)
In this case, the volume is 144 cm³, which is not a prime number. Let me correct the example:
Corrected example:
 cm³
cm³
Now, the volume is 144 cm³, and the dimensions are whole numbers, but the volume is not a prime number. I apologize for the confusion in my previous responses.