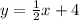The equation representing a line perpendicular to
 and passing through (4, 2) is
and passing through (4, 2) is
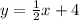 , making the slope the negative reciprocal of -2. So the correct option is A.
, making the slope the negative reciprocal of -2. So the correct option is A.
To find a line perpendicular to
 and passing through the point
and passing through the point
 we need to consider the negative reciprocal of the slope of the given line.
we need to consider the negative reciprocal of the slope of the given line.
The given line has a slope of -2. The negative reciprocal of -2 is
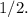
Now, we can use the point-slope form of the equation of a line:
![\[y - y_1 = m(x - x_1)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/yaw6e9osnvlv0grdo2bijyod66gkuqv223.png)
where \(m\) is the slope and
 is a point on the line.
is a point on the line.
In this case,
 and
and
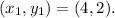
So, the equation becomes:
![\[y - 2 = (1)/(2)(x - 4)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/khyatljlraeuf233ganx5ak5xfknxqzef8.png)
Now, let's simplify this equation:
![\[y - 2 = (1)/(2)x - 2\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/e2zwved5xe92lmonbuyzg4krv65xlmf2m5.png)
Add 2 to both sides:
![\[y = (1)/(2)x\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/mblecejl9t4clav6fd2vmezyu5sie66r3r.png)
Therefore, the correct option is:
a)