Final answer:
The focus of the parabola y = x²/2 is ((0, 1/4)) and the directrix is the horizontal line y = 1/4.
The answer is option ⇒b) Focus: ((0, 1/4)), Directrix: (y = 1/4)
Step-by-step explanation:
To find the focus and directrix of the parabola y = x²/2, we can use the standard form of a parabolic equation:
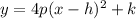
In this case, the vertex (h, k) is (0, 0) and the coefficient 4p determines the distance between the focus and the vertex, as well as the distance between the directrix and the vertex.
Comparing the given equation y = x²/2 to the standard form, we can see that 4p = 1/2, which means p = 1/8.
The focus is located at a distance p above the vertex, so the focus is at (0, 1/8).
The directrix is located at a distance p below the vertex, so the directrix is the horizontal line y = -1/8.
The answer is option ⇒b) Focus: ((0, 1/4)), Directrix: (y = 1/4)