Question

Write an equation for an eclipse centered at the origin, which has the foci at (±12,0) and vertices at (±13,0).

Answer 1

The equation for an ellipse centered at the origin, with foci at (±12,0) and vertices at (±13,0), is
`\((x^2)/(169) + (y^2)/(25) = 1\).`

Step-by-step explanation:

To derive the equation for the given ellipse, we consider the properties of ellipses in standard form. The general equation for an ellipse centered at the origin is
`\((x^2)/(a^2) + (y^2)/(b^2) = 1\), where \(a\) and \(b\)` are the semi-major and semi-minor axes, respectively. The foci of the ellipse are located along the x-axis at the points (±12,0), and the vertices are at (±13,0). The distance from the center to the foci is given by
`\(c\),` and the distance from the center to the vertices is given by
`\(a\).`

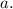
By inspection, we find that
`\(a = 13\`) (distance to vertices) and
`\(c = 12\)`(distance to foci). The semi-minor axis,
`\(b\),` is determined by the relationship
`\(b = √(a^2 - c^2)\).` Substituting the values, we get
`\(b = √(13^2 - 12^2) = 5\).`Thus, the equation for the ellipse is
`\((x^2)/(169) + (y^2)/(25) = 1\).`

In summary, the equation
`\((x^2)/(169) + (y^2)/(25) = 1\)` represents an ellipse centered at the origin, with foci at (±12,0) and vertices at (±13,0). The process involves understanding the geometric properties of ellipses and applying the formula for the semi-minor axis based on the given foci and vertices.