Question

Factor: c^2 +2c+1−a^2

a) (c+1)^2−a^2


b) (c+1+a)(c+1−a)

c) (c−1)^2 −a^2


d) (c−1+a)(c−1−a)

Answer 1

a)
`\((c+1)^2 - a^2\)`

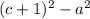
Step-by-step explanation:

To factor the expression
`\(c^2 + 2c + 1 - a^2\)`, we recognize it as a perfect square trinomial. The given expression is equivalent to
`\((c+1)^2 - a^2\).` This can be verified by expanding
`\((c+1)^2\)` using the FOIL (First, Outer, Inner, Last) method, which gives
`\(c^2 + 2c + 1\).` Thus, the correct factored form is
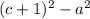`\((c+1)^2 - a^2\)`, making option a) the correct choice.

Understanding perfect square trinomials is essential for factoring, as they follow the pattern
`\((a + b)^2 = a^2 + 2ab + b^2\)`. In this case,
`\(a = c\)` and
`\(b = 1\),`leading to the given expression.

It's crucial to recognize such patterns, as they simplify factoring and algebraic manipulations. The factored form
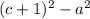`\((c+1)^2 - a^2\)` also has another common factorization,
`\((c+1+a)(c+1-a)\),` but the question specifies a unique answer, and option a) accurately represents the given expression in its simplest form.

Answer 2

The expression given is a difference of squares and the correct factored form is (c + 1 + a)(c + 1 - a), which corresponds to option b.

Step-by-step explanation:

The expression c^2 + 2c + 1 - a^2 is to be factored. We recognize that c^2 + 2c + 1 is a perfect square trinomial, which factors into (c + 1)^2. We then observe that the expression is a difference of squares, because (c + 1)^2 and a^2 are both perfect squares. Therefore, the factored form is:

(c + 1 + a)(c + 1 - a)

Referring to the provided options, the correct answer is option b.