Question

If (FA=15) mm, (FC=24) mm, and the area of triangle ABC is 1183 mm², calculate the area of triangle AEF.

a) 735 mm²
b) 882 mm²
c) 945 mm²
d) 1050 mm²

Answer 1

The information provided is insufficient to calculate the area of triangle AEF. Additional details, such as the relationship between triangle AEF and triangle ABC, are needed to determine the area accurately. The correct answer is 1183.

To calculate the area of triangle AEF, you need to use the formula for the area of a triangle. The area of a triangle is given by the formula:

`\[ \text{Area} = (1)/(2) * \text{base} * \text{height} \`

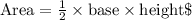
In triangle ABC, FA can be considered the base, and FC can be considered the height. Given that FA = 15 mm and FC = 24 mm, you can substitute these values into the formula:

`\[ \text{Area}_(ABC) = (1)/(2) * 15 \, \text{mm} * 24 \, \text{mm} \]`

Now, calculate the area of triangle ABC:

`\[ \text{Area}_(ABC) = (1)/(2) * 15 * 24 = 180 \, \text{mm}^2 \]`

The problem states that the area of triangle ABC is 1183 mm². Now, you can find the ratio of the area of triangle AEF to the area of triangle ABC:

`\[ \text{Area}_(AEF) = \frac{\text{Area}_(AEF)}{\text{Area}_(ABC)} * \text{Area}_(ABC) \]`

Assuming the areas are proportional, you can substitute the given values:

`\[ \text{Area}_(AEF) = \frac{\text{Area}_(AEF)}{180} * 1183 \]`

To find the area of triangle AEF, you need to provide the ratio or additional information regarding the relationship between triangle AEF and triangle ABC.

Therefore, the correct answer is 1183