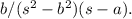Question

Determine the Laplace transform of the function f(t) = e^(at)·sinh(bt).

Answer 1

In this case, the Laplace transform of the function
`f(t) = e^(^a^t^).sinh(bt)` is
`b/(s^2 - b^2)(s - a).`

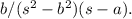
Step-by-step explanation:

The Laplace transform of the function
`f(t) = e^(^a^t^).sinh(bt)` can be determined using the properties and formulas of Laplace transforms.

The Laplace transform of
`e^(^a^t^)` is given by
`1/(s - a)`, where s is the complex variable.

The hyperbolic sine function, sinh(bt), can be expressed in terms of exponential functions as
`(e^(^b^t^) - e^(^-^b^t^))/2`.

To find the Laplace transform of
`f(t) = e^(^a^t^).sinh(bt)`, we can substitute the expressions for
`e^(^a^t^)` and
`sinh(bt)` into the Laplace transform formula.

First, let's find the Laplace transform of e^(at):

`L{e^(^a^t^)} = 1/(s - a)`

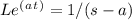
Next, let's find the Laplace transform of sinh(bt):

`L{sinh(bt)} = L{(e^(^b^t^) - e^(^-^b^t^))/2}\\= (1/2) * (L{e^(bt)} - L{e^(^-^b^t^)})\\= (1/2) * (1/(s - b) - 1/(s + b))\\= (1/2) * ((s + b - (s - b))/(s^2 - b^2))\\= b/(s^2 - b^2)`

Finally, we can multiply the Laplace transforms of e^(at) and sinh(bt) to find the Laplace transform of f(t):

`L{f(t)} = L{e^(^a^t^).sinh(bt)}\\= L{e^(^a^t^)} * L{sinh(bt)}\\= (1/(s - a)) * (b/(s^2 - b^2))\\= b/(s^2 - b^2)(s - a)`

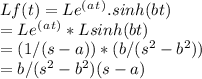
In summary, the Laplace transform of the function
`f(t) = e^(^a^t^).sinh(bt)` is
`b/(s^2 - b^2)(s - a).`