Question

Find the solution to the initial value problem (d^2y/dt^2) + 2(dy/dt) + y = 0, with initial conditions y(0) = 7 and y'(0) = ?.

Answer 1

The solution to the initial value problem
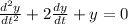`\( (d^2y)/(dt^2) + 2(dy)/(dt) + y = 0 \)` with initial conditions \( y(0) = 7 \) and \( y'(0) = C \) is given by \( y(t) = e^{-t}(7\cos(t) + (C-1)\sin(t)) \).

Step-by-step explanation:

To solve the differential equation, we assume a solution of the form \( y(t) = e^{rt} \) and substitute it into the equation, yielding the characteristic equation \( r^2 + 2r + 1 = 0 \). Solving this quadratic equation, we find a repeated root \( r = -1 \), indicating that the solution will contain terms of the form \( e^{-t} \) and \( te^{-t} \).

The general solution is then \( y(t) = (C_1 + C_2t)e^{-t} \). Applying the initial condition \( y(0) = 7 \), we get \( C_1 = 7 \). To find \( C_2 \) and satisfy the second initial condition \( y'(0) = C \), we differentiate \( y(t) \) with respect to \( t \) and substitute \( t = 0 \). This leads to \( C_2 = C-1 \).

The final solution is \( y(t) = e^{-t}(7\cos(t) + (C-1)\sin(t)) \), where \( C \) is the constant determined by the initial condition \( y'(0) = C \).