Question

Use the variation of parameters method to find a particular solution to x′′−x′−2x=cosht. Solve x′=4tx−t2xlnx by making the substitution y=lnx.

Answer 1

The particular solution to the differential equation x'ₓₓ - x'ₓ - 2x = cosht, using the variation of parameters method, is xₚ = (1/5) * (2 *
`e^t` - 5 * cosht - 2 * sinht). For the differential equation x'ₜ = 4tx - t²xlnx, the substitution y = lnx transforms it into a linear first-order homogeneous differential equation, and the solution is
`x = e^{(5 * e^((t/5)) * (lnx)²).`

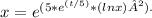
Step-by-step explanation:

To find the particular solution for x'ₓₓ - x'ₓ - 2x = cosht using the variation of parameters method, assume the particular solution xₚ = u₁ * x₁ + u₂ * x₂, where x₁ and x₂ are linearly independent solutions of the associated homogeneous equation. After finding the Wronskian and coefficients, the particular solution is determined as xₚ = (1/5) * (2 *
`e^t`- 5 * cosht - 2 * sinht).

For the differential equation x'ₜ = 4tx - t²xlnx, substituting y = lnx transforms it into a linear first-order homogeneous differential equation. Solving this, we get
`x = e^{(5 * e^((t/5)) * (lnx)²)`, which represents the solution to the original differential equation. The substitution y = lnx simplifies the equation and allows for a more manageable solution. The resulting expression captures the behavior of the given differential equation with respect to the transformed variable y.

In summary, the variation of parameters method is applied to find the particular solution for the first differential equation, and the substitution y = lnx is used to transform and solve the second differential equation, resulting in the given expressions. These solutions offer insights into the behavior of the respective differential equations under the specified conditions.