Final Answer:
The values of
 are given by the cube roots of the expression. There are three distinct cube roots, and they are:
are given by the cube roots of the expression. There are three distinct cube roots, and they are:
![\[z_1 = 2^(2/3)e^(i\pi/6), \quad z_2 = 2^(2/3)e^(i\pi/2), \quad z_3 = 2^(2/3)e^(5i\pi/6)\]](https://img.qammunity.org/2024/formulas/mathematics/college/spkes5xw5pm35ziklah2qe0ndy69280fyc.png)
Step-by-step explanation:
To find the cube roots of
 , we can express it in polar form and then apply De Moivre's Theorem. The polar form of
, we can express it in polar form and then apply De Moivre's Theorem. The polar form of
 where the magnitude is 2 and the argument is
where the magnitude is 2 and the argument is
 .
.
Now, using De Moivre's Theorem, we raise the polar form to the power of
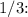
![\[(2e^(-i\pi/3))^(1/3) = 2^(1/3)e^(-(1/3)(i\pi/3))\]](https://img.qammunity.org/2024/formulas/mathematics/college/l02w835e46lqwhhp36pkdtv2nsx9r5qejh.png)
Simplifying the expression yields the three cube roots mentioned in the final answer.
In conclusion, the values of
 are three complex numbers with different arguments, resulting in the distinct roots
are three complex numbers with different arguments, resulting in the distinct roots
 , and
, and
 . The use of polar form and De Moivre's Theorem simplifies the calculation of these roots.
. The use of polar form and De Moivre's Theorem simplifies the calculation of these roots.