Question

A particle moves with position function r(t) = ti +2e' j+e-'.

a) Find the tangential component of the acceleration vector.
b) Find the normal component of the acceleration vector.

Answer 1

• a) The tangential component of the acceleration vector is
  `|aT| = √((4e^2t + 16e^4t).)`
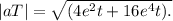
• b) The normal component of the acceleration vector is 0.

Step-by-step explanation:

a) To find the tangential component of the acceleration vector, we need to differentiate the position function twice with respect to time.

Given:

Position function
`r = (2e^t)i + tj + (e^2t)k`

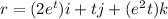
1. Differentiate the position function with respect to time to find the velocity vector v:

`v = dr/dt = d/dt[(2e^t)i + tj + (e^2t)k]\\= (2e^t)i + j + (2e^2t)k`

2. Differentiate the velocity vector with respect to time to find the acceleration vector a:

`a = dv/dt = d/dt[(2e^t)i + j + (2e^2t)k]\\= (2e^t)i + 0j + (4e^2t)k`

3. The tangential component of the acceleration vector is the component of the acceleration vector in the direction of the velocity vector. To find it, we can project the acceleration vector onto the velocity vector.

The dot product of two vectors A and B is given by A · B = |A| |B| cos θ, where θ is the angle between the two vectors.

In this case, the velocity vector v is
`(2e^t)i + j + (2e^2t)k`, and the acceleration vector a is
`(2e^t)i + 0j + (4e^2t)k`.

The magnitude of the velocity vector
`|v| = √([(2e^t)^2 + 1^2 + (2e^2t)^2]) = √((4e^2t + 1 + 4e^4t))`

The magnitude of the acceleration vector
`|a| = √([(2e^t)^2 + 0^2 + (4e^2t)^2]) = √((4e^2t + 16e^4t))`

The angle θ between the velocity vector and the acceleration vector is 0 degrees because they are parallel.

Therefore, the tangential component of the acceleration vector is given by:

|aT| = |a| cos θ =
`|a| = √((4e^2t + 16e^4t))`

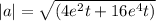
b) The normal component of the acceleration vector is the component of the acceleration vector perpendicular to the velocity vector. To find it, we can use the formula for the magnitude of the cross product of two vectors.

The cross product of two vectors A and B is given by |A × B| = |A| |B| sin θ, where θ is the angle between the two vectors.

In this case, the velocity vector v is
`(2e^t)i + j + (2e^2t)k`, and the acceleration vector a is
`(2e^t)i + 0j + (4e^2t)k`.

The magnitude of the cross product of the velocity vector and the acceleration vector |v × a| = |v| |a| sin θ = 0 because they are parallel.

Therefore, the normal component of the acceleration vector is 0.

Your question is incomplete, but most probably the full question was:

A particle moves with position function
`r = (2e^t)i + (t)j +(e^2t)k`.

a) Find the tangential component of the acceleration vector.

b) Find the normal component of the acceleration vector.