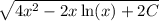Question

Find the general solution of the diffential equation y ′ = 2−lnx/(y/x +6x)​

Answer 1

To find the general solution of the given first-order differential equation y' =
`(2 - \ln(x))/((y)/(x) + 6x)\)`, we'll use separation of variables. The general solution to the y' =
`(2 - \ln(x))/((y)/(x) + 6x)\)` is y = ±
`√(4x^2 - 2x\ln(x) + 2C)`

Step-by-step explanation:

To find the general solution of the given first-order differential equation y' =
`(2 - \ln(x))/((y)/(x) + 6x)\)`, we'll use separation of variables.

First, express the equation in a more suitable form:

y' =
`(2 - \ln(x))/((y)/(x) + 6x)`

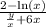
Multiply both sides by y/x + 6x to separate variables:

y'(y/x + 6x) = 2 - ln(x)

Distribute y' on the left side:

y' ·
`(y)/(x)` + y' · 6x = 2 - ln(x)

Now, separate variables and integrate:

`\[\int (y)/(x) \,dy + \int 6x \,dy = \int (2 - \ln(x)) \,dx\]`

Integrate each term:

`\[(1)/(2)` y² + 3x² = 2x - x ln(x) + C

Here, C is the constant of integration.

Now, rearrange the equation to solve for y:

y² = 4x² - 2x ln(x) + 2C

Finally, take the square root of both sides:

y = ±
`√(4x^2 - 2x\ln(x) + 2C)`

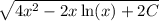
So, the general solution to the given differential equation is:

y = ±
`√(4x^2 - 2x\ln(x) + 2C)`