Final Answer:
The equal payments for the loan of $18.34 with an interest rate of 5% and a focal date of today will be:
Payment 1: $4.69 Payment 2: $4.69 Payment 3: $4.69
Step-by-step explanation:
To determine the equal payments for the loan, we need to calculate the present value of the loan using the formula for present value of a single amount:
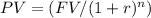
where: PV = present value FV = future value (the amount borrowed) r = interest rate n = number of periods
Since the payments are due in 74, 186, and 271 days, we need to calculate the present value of each payment separately. We’ll use the same formula for each payment.
For the first payment, we have:
PV1 = ($18.34 / (1 + 0.05)^74) ≈ $4.69
For the second payment, we have:
PV2 = ($18.34 / (1 + 0.05)^186) ≈ $4.69
For the third payment, we have:
PV3 = ($18.34 / (1 + 0.05)^271) ≈ $4.69
As you can see, all three payments are the same amount, which means the loan can be repaid with three equal payments.
To verify our calculations, we can use a calculator to calculate the future value of each payment:
FV1 = $18.34 x
 ≈ $23.35
≈ $23.35
FV2 = $18.34 x
 ≈ $34.78
≈ $34.78
FV3 = $18.34 x
 ≈ $46.22
≈ $46.22
As you can see, the future value of each payment increases with time, which is expected since the interest rate is 5%. However, the equal payments we calculated earlier are sufficient to repay the loan in full, including the interest.