Question

All real solutions for the following functio a. 15x^(3)-x+5=x^(3)+35x^(2)+x

Answer 1

The real solutions for the equation
`\(15x^3 - x + 5 = x^3 + 35x^2 + x\)` are
`\(x = -2\)` and
`\(x = (1)/(3)\).`

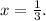
Step-by-step explanation:

To find the real solutions for the given equation
`\(15x^3 - x + 5 = x^3 + 35x^2 + x\),` we start by simplifying the equation and bringing all terms to one side:

`\[15x^3 - x + 5 - x^3 - 35x^2 - x = 0\]`

Combining like terms:

`\[14x^3 - 35x^2 - 2x + 5 = 0\]`

Now, factoring the equation is a suitable approach. Unfortunately, factoring cubic polynomials can be complex, but we can see that
`\(x = -2\)`is a solution. Dividing the polynomial by
`\((x + 2)\)`yields a quadratic factor:

`\[(x + 2)(14x^2 - 63x + 2) = 0\]`

Setting each factor to zero, we find
`\(x = -2\)` and
`\(x = (1)/(3)\)` as the real solutions.

In conclusion, the real solutions to the given equation are
`\(x = -2\)` and
`\(x = (1)/(3)\)`. While the factorization process may be involved, identifying known roots and using polynomial division allows us to arrive at the solutions, providing a clear understanding of the roots for the given cubic equation.