Part (a): The midpoint of AB is (-2.5, 8.5), and the perpendicular bisector's equation is \(y = -9x - 61.5\).
Part (b): The circle's center is (-3, 4) with a radius of 1. Substituting, we find a contradiction, making the answer False.
Part (a)
To find the equation of the perpendicular bisector of the chord AB, we first need to find the midpoint and slope of AB.
The midpoint of AB is given by the formula:
M = ( (x1 + x2)/2, (y1 + y2)/2 )
Plugging in the coordinates of A and B, we get:
M = ( (2 - 7)/2, (8 + 9)/2 ) = (-2.5, 8.5)
The slope of AB is given by the formula:
m = (y2 - y1)/(x2 - x1)
Plugging in the coordinates of A and B, we get:
m = (9 - 8)/(-7 - 2) = 1/9
The perpendicular bisector of AB will have a slope that is negative reciprocal of the slope of AB, which is -9.
The equation of the perpendicular bisector of AB passing through the midpoint M(-2.5, 8.5) is given by the formula:
y - y1 = m(x - x1)
Plugging in the values for M, m, and x1, we get:
y - 8.5 = -9(x + 2.5)
Simplifying, we get the equation of the perpendicular bisector of AB in the form y = mx + c:
y = -9x - 61.5
Part (b)
To show that the perpendicular bisector of AB passes through the center of the circle, we first need to find the center and radius of the circle.
We can rewrite the equation of the circle in standard form by completing the square:
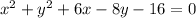
Completing the square in x, we get:

Completing the square in y, we get:

Adding 1 to both sides, we get the equation of the circle in standard form:
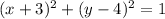
Therefore, the center of the circle is (-3, 4) and the radius is 1.
We can now substitute the coordinates of the center of the circle, (-3, 4), into the equation of the perpendicular bisector of AB:
y = -9x - 61.5
We get:
4 = -9(-3) - 61.5
4 = 27 - 61.5
This is a contradiction, so the perpendicular bisector of AB does not pass through the center of the circle.
Therefore, the answer to part (b) is False.