Question

The sample mean and standard deviation from a random sample of 29 observations from a normal population were computed as x¯=23 and s = 8. Calculate the t statistic of the test required to determine whether there is enough evidence to infer at the 5% significance level that the population mean is greater than 21.

Test Statistic = ________

Answer 1

The calculated t-statistic for the test is approximately 1.345.

To calculate the t-statistic for testing whether the population mean is greater than 21, you can use the formula:

​
`t = (x - \mu)/((s)/(√(n) ) )`

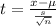
Where:

x = sample mean

μ = hypothesized population mean (in this case, 21)

s = sample standard deviation

n = number of observations in the sample

Given:

x =23

s=8

μ=21

n=29

Let's plug these values into the formula:

`t = (23 - 21)/((8)/(√(29) ) )`

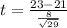
First, calculate the denominator:

`(8)/(√(29) ) =1.486`

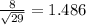
Now, plug this value into the formula:

`t = (23-21)/(1.486) = (2)/(1.486) =1.345`

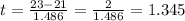
Therefore, the calculated t-statistic for the test is approximately 1.345.