Question

A random sample of size 10 was taken from a normal population. a 99% confidence interval for the mean of the population was computed based on the sample data. the confidence interval for the mean was calculated to be (1.88, 2.42). what is the t value that was used in the computation? round your answer to two decimal places.

Answer 1

The t-value used in the computation of the confidence interval is 3.25.

To find the t-value used in the computation of the confidence interval, we can use the formula for the confidence interval of the mean:

Confidence Interval=
`x + (t . (s)/(√(n) ) )`

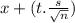
Given:

Confidence Interval for the mean = (1.88, 2.42)

Sample size (n) = 10

The formula for the margin of error in a t-distribution is:

Margin of Error=
`t . (s)/(√(n) )`

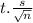
The width of the confidence interval is the difference between the upper and lower limits:

Width of Interval=Upper Limit−Lower Limit

Width of Interval=2.42−1.88=0.54

The margin of error is half of the width of the interval:

Margin of Error=
`(width of interval)/(2) = (0.54)/(2)`=0.27

Now, we need to find the t-value for a 99% confidence interval using a t-table or calculator. The t-value is such that 99% of the area under the t-distribution curve lies within this range.

From the t-table for a two-tailed test with a 99% confidence level and 9 degrees of freedom (since n−1=10−1=9):

The t-value is approximately 3.25.

Therefore, the t-value used in the computation of the confidence interval is 3.25.