Question

Nadya thought of a number. She gives one clue about her number in each of the parts below. Nadya's first clue is that her number is a whole number N, such that 20

Answer 1

To calculate the probability that Nadya's number is 27 given that it is a whole number between 20 and 60 inclusive, we follow these steps:

1. Determine the total number of whole numbers in the range.

2. Identify the number of favorable outcomes.

3. Calculate the probability.

Step 1: Total Number of Whole Numbers in Range

The range is from 20 to 60 inclusive. So, we count every whole number from 20 up to and including 60.

`\( Total\ Numbers = 60 - 20 + 1 \)`

Step 2: Identify Favorable Outcomes

The number of favorable outcomes is the count of the number 27 in that range. Since 27 is only one number, there is only one favorable outcome.

`\( Favorable\ Outcomes = 1 \)`

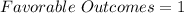
Step 3: Calculate Probability

The probability
`\( P \)`of an event is given by the ratio of the number of favorable outcomes to the total number of possible outcomes.

`\( P = (Favorable\ Outcomes)/(Total\ Numbers) \)`

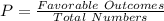
Now we substitute in the values and calculate the probability.

The probability that Nadya's number is 27, given that it is a whole number between 20 and 60 inclusive, is approximately
`\( 0.0244 \) or \( (1)/(41) \)` when expressed as a fraction.

Here's the detailed calculation:

1. Total Number of Whole Numbers in Range:

`\[ Total\ Numbers = 60 - 20 + 1 = 41 \]`

2. Identify Favorable Outcomes:

`\[ Favorable\ Outcomes = 1 \] (since we are only looking for the number 27)`

3. Calculate Probability:

`\[ P = (Favorable\ Outcomes)/(Total\ Numbers) = (1)/(41) \approx 0.0244 \`]

complete question given below:

Nadya thought of a number. She gives one clue about her number in each of the parts below. Nadya's first clue is that her number is a whole number N, such that 20 . What is the probability that Nadya's number is 27?

Answer 2

The question deals with the calculation of the number of radioactive nuclei remaining after time t, based on the half-life t1/2. However, part of the question seems to be missing, making it difficult to provide a complete answer. The numerical sequence provided does not appear to relate to the concept of radioactive decay.

Step-by-step explanation:

The question seems incomplete, but based on the provided context, it involves the concept of radioactive decay and the calculation of the number of radioactive nuclei remaining after a certain amount of time. The half-life, represented as t1/2, is the time required for half of the radioactive nuclei to decay. The standard formula for radioactive decay, which demonstrates the relationship between the initial number of nuclei (No) and the number remaining after time t (N1), is essential for these calculations.

The incomplete numerical sequence at the end does not immediately correlate with the given information on radioactive decay. However, you mentioned that one should ignore typos or irrelevant parts, which suggests that the sequence might not be related to the question at hand.