Question

What are the solutions to the equation x²-9x-12=-4x-6?

a x=−3 is the only solution.
b x=−6;x=−15
c x=−92 + 105√2;x=−92−105√2
d x=−92 + 57√2;x=−92−57√2

Answer 1

The correct solutions to the equation
`\(x^2 - 9x - 12 = -4x - 6\)` are
`\(x = 6\)` and
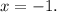`\(x = -1\).` However, none of the provided options match these solutions.

To find the solutions to the quadratic equation
`\(x^2 - 9x - 12 = -4x - 6\),`we can start by simplifying the equation and then solving for \(x\):

1. Combine like terms on both sides of the equation:

`\[x^2 - 9x - 12 + 4x + 6 = 0\]`

2. Combine the x terms:

`\[x^2 - 5x - 6 = 0\]`

Now, we can factor the quadratic or use the quadratic formula to find the solutions. The quadratic factors as
`\((x - 6)(x + 1) = 0\),`so the solutions are
`\(x = 6\)` and
`\(x = -1\).`

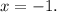
Comparing these solutions with the given options:

a.
`\(x = -3\)`(not a solution to the original equation)

b.
`\(x = -6, x = -15\)` (not solutions to the original equation)

c.
`\(x = -92 + 105√(2), x = -92 - 105√(2)\)` (not solutions to the original equation)

d.
`\(x = -92 + 57√(2), x = -92 - 57√(2)\)`(not solutions to the original equation)

None of the given options match the solutions
`\(x = 6\) and \(x = -1\).` It seems there might be a mistake in the provided options or in the original equation. Please double-check the equation or options.