The completed statements can be presented as follows;
f(t) =
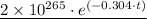
The number of polio cases decreases by 30.4% per year
Predicted number of polio cases in 2017, are about 101 polio cases
Predicted year in which there will be 1 polio case in the year 2032
Half-life of the number of polio cases is; 4 years
The steps by which the above values are found are presented as follows;
The scatter diagram obtained using the data in the table indicates that the square of the R-squared value for the linear model is R² = 0.7195, and the R-squared for the exponential model is; R² = 0.9894, which indicates that it is better to model the data using an exponential model
The equation for f, obtained using the exponential model can be presented as follows;
f(t) = 2×10²⁶⁵×
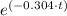
The exponential model indicates that the number of polio cases decreases by 30.4% per year
The number of polio cases in 2017, can be found by plugging in 2017 in the the equation, f(t) = 2×10²⁶⁵×
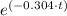 , as follows;
, as follows;
f(2017) = 2×10²⁶⁵×

2×10²⁶⁵×
 ≈ 0.1013
≈ 0.1013
Therefore, the number of polio cases in 2017 is about; 1000 × 0.1013 = 101.3
The year in which there will be 1 case of polio, can be found using the following equation
f(t) = 2×10²⁶⁵×
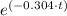
f(t) = 1
2×10²⁶⁵×
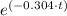 = 1
= 1
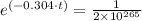
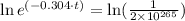
-0.304·t =

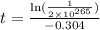
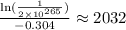
The year in which there will be 1 polio case is about 2032
The approximate half life can be found as follows;
The number of polio cases in 1988 is 350,000
When the number is half the above amount or 350,000/2 = 175,000, we get;
2 × 10²⁶⁵ ×
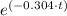 = 175
= 175
ln
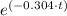 =
=
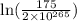
-0.304·t =
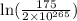
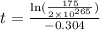
t ≈ 1992
Therefore, the half life is about 1992 - 1988 = 4 years