To solve side a of the triangle, we can use the Law of Cosines. Therefore, side a is approximately 12.67.
To solve the triangle, we can use the Law of Cosines. This states that:
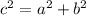 - 2abcos(C), where a, b, and c are the lengths of the sides and C is the angle opposite side c.
- 2abcos(C), where a, b, and c are the lengths of the sides and C is the angle opposite side c.
In this case, we are given angle A = 52°, side b = 14, and side c = 6. To find side a, we can use the equation:
 - 2bccos(A).
- 2bccos(A).
Plugging in the values, we get:
 - 2(14)(6)cos(52°).
- 2(14)(6)cos(52°).
 -168cos(52)
-168cos(52)
a=

Solving for a, we find a ≈ 12.67.
The probable question may be:"Solve side a the triangle. Given: A = 52∘, , b = 14, , c = 6"