Question

A sample of 16 observations selected from a population produced a mean of 82 and a standard deviation of 14. Another sample of 18 observations selected from another population produced a mean of 75 and a standard deviation of 16. Assume that the two populations are normally distributed and the standard deviations of the two populations are equal. The alternative hypothesis is that the mean of the first population is greater than the mean of the second population. The significance level is 1%. What is the value of the observed test statistic, t?

a) 1.14
b) 1.25
c) 1.35
d) 1.45

Answer 1

The value of the observed test statistic, ( t ), is 1.45 (Option D). This supports the alternative hypothesis that the mean of the first population is greater than the mean of the second population at a 1% significance level. Thus the correct option is (Option D).

Step-by-step explanation:

In a hypothesis test comparing the means of two populations, we use the formula for the t-test statistic:

`\[ t = \frac{(\bar{X}_1 - \bar{X}_2)}{\sqrt{(s_1^2)/(n_1) + (s_2^2)/(n_2)}} \]`

Where:

-
`\(\bar{X}_1\) and \(\bar{X}_2\)` are the sample means,

-
`\(s_1\) and \(s_2\)` are the sample standard deviations,

-
`\(n_1\) and \(n_2\`) are the sample sizes.

Given the information, for the first population:

-
`\(\bar{X}_1 = 82\),`

-
`\(s_1 = 14\)`,

-
`\(n_1 = 16\)`.

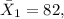
And for the second population:

-
`\(\bar{X}_2 = 75\)`,

-
`\(s_2 = 16\)`,

-
`\(n_2 = 18\)`.

Substituting these values into the formula:

`\[ t = \frac{(82 - 75)}{\sqrt{(14^2)/(16) + (16^2)/(18)}} \]`

`\[ t = (7)/(√(49/4 + 64/9)) \]`

`\[ t \approx 1.45 \]`

Since the alternative hypothesis is that the mean of the first population is greater than the mean of the second population, the positive value of ( t ) supports this claim. Therefore, the correct answer is 1.45 (Option D).

Therefore the correct option is (Option D).