Question

Find the value of an investment of $2000 after one year, if the annual rate is 12% and the interest is compounded quarterly.

Answer 1

The value of the investment after one year, compounded quarterly at an annual rate of 12%, is approximately $2245.18.

Step-by-step explanation:

Compound interest is calculated using the formula A = P(1 + r/n)^(nt), where:

A = the future value of the investment

P = the principal amount ($2000 in this case)

r = the annual interest rate (12% or 0.12)

n = the number of times the interest is compounded per year (quarterly compounding means n = 4)

t = the time the money is invested for (1 year)

Using the formula, we get A = 2000
`* (1 + 0.12/4)^(4*1) = 2000 * (1 + 0.03)^4 = 2000 * (1.03)^4 ≈ $2245.18.`

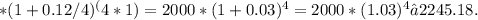
Explanation Breakdown:

Compound interest, computed using the formula A = P(1 + r/n)^(nt), determines the future value of an investment.

For this scenario, the principal amount (P) is $2000, the annual interest rate (r) is 12% or 0.12, and the interest is compounded quarterly (n = 4) over a period of 1 year (t = 1).

Applying the formula, we substitute the values to find the future value (A) of the investment:
`A = 2000 * (1 + 0.12/4)^(4*1).`

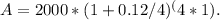
Solving further, we simplify the equation:
`A = 2000 * (1 + 0.03)^4.`

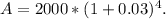
Upon calculation, the future value of the investment is approximately $2245.18 after one year.

Thus, with quarterly compounding at an annual rate of 12%, the initial investment of $2000 grows to approximately $2245.18 after one year. Compound interest allows for the accrual of interest on both the initial principal and the interest earned, resulting in a higher return than simple interest.