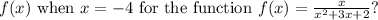When
 the function evaluates to
the function evaluates to
 Thus,
Thus,
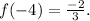
To find the value of
 when
when
 for the given function
for the given function
 , substitute
, substitute
 into the expression:
into the expression:
![\[ f(-4) = (-4)/((-4)^2 + 3(-4) + 2) \]](https://img.qammunity.org/2024/formulas/mathematics/college/l7rqisgzeez30x3rgnjn39d9j2qaqsbjr0.png)
Firstly, evaluate the expression in the denominator:
![\[ (-4)^2 + 3(-4) + 2 = 16 - 12 + 2 = 6 \]](https://img.qammunity.org/2024/formulas/mathematics/college/sof6ytfsoy34fsktkz9a5yqzxgmpipl163.png)
Now, substitute this value back into the original expression:
![\[ f(-4) = (-4)/(6) \]](https://img.qammunity.org/2024/formulas/mathematics/college/5rdzy1gzjfzain2ne3dsuaw263l1enz44e.png)
To simplify further, we can divide both the numerator and the denominator by their greatest common divisor, which is 2:
![\[ f(-4) = (-2)/(3) \]](https://img.qammunity.org/2024/formulas/mathematics/college/5mqmgfgrckbgreptwp5azlj1ehk26kid13.png)
So, when
 , the function
, the function
 evaluates to
evaluates to
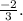 Therefore, the answer to the question is that the value of
Therefore, the answer to the question is that the value of
 when
when
 for the given function is
for the given function is
This process demonstrates how to use the provided function to compute specific values, in this case, when

The probable question maybe:
What is the value of