○=> Solution (2) :
This triangle(Fig. 9.120) is a right angled triangle.
So, the three angles in this triangle are :
▪︎angle 90°, angle 63° and angle y.
Sum of all angles in a triangle = 180°
Which means :
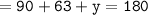
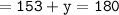
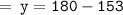
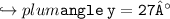
Since the sum of all angles equals 180°[90+63+27=180] we can conclude that we have found out the correct measure of angle y.
▪︎Therefore, the measure of angle y = 27°
○=> Solution (3) :
The triangle in Fig. 9. 121 is a right angled triangle.
So, the angles in this triangle are :
▪︎angle 90°, angle 28.3° and angle z.
Sum of all angles in a triangle = 180°
Which means :
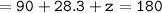
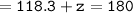
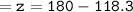
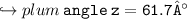
Since the sum of all angles equals 180°[90+28.3+61.7=180°] we can conclude that we have found out the correct measure of angle z.
▪︎Therefore, the measure of angle z = 61.7°
○=> Solution (4) :
The triangle in Fig. 9. 122 is a right angled triangle.
So, the angles in this triangle are :
▪︎angle 90°, angle 45.8° and angle x.
Sum of all angles in triangle = 180°
Which means :
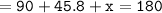
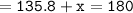

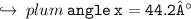
Since the sum of all angles equals 180°[90+45.8+44.2=180°] we can conclude that we have found out the correct measure of angle x.
▪︎Therefore, the measure of angle x = 44.2°
○=> Solution (5) :
The triangle in Fig. 9.123 is a right angled triangle.
So, the angles in this triangle are :
▪︎angle 90°, angle 35.7° and angle y.
Sum of all angles in a triangle = 180°
Which means :

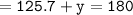
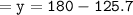

Since the sum of all angles equals 180°[90+35.7+54.3=180°] we can conclude that we have found out the correct measure of angle y.
▪︎Therefore, the measure of angle y = 54.3°
○=> Solution (6) :
No, angle x is not twice of angle y. As we know the value of angle x in fig. 9.122 is equal to 44.2°. And the value of angle y in fig. 9.123 is equal to 54.3°. Since the measure of angle x is lesser than angle y it cannot be twice as much as angle y.
Therefore, angle x is not twice as much as angle y since angle x < angle y.