Question

What is the slope of the line that contains both points of intersection when the equations (y = 2(x – 4)² – 2) and (y = (x – 3)²) are plotted in the xy-plane?

a. 2
b. 1
c. -1
d. -2

Answer 1

The slope of the line that contains both points of intersection when the equations
`y= 2(x-4)^ 2 -2` and
`y= (x-3)^(2)` are plotted in the xy-plane is d. -2.

Step-by-step explanation:

The given equations represent quadratic functions that intersect at certain points in the xy-plane. To find the points of intersection, set the equations equal to each other:

`2(x-4)^ 2 -2 =(x-3)^(2)`.

Solving this equation yields two points of intersection. After determining the x-coordinates of these points, calculate the corresponding y-coordinates by substituting them back into either of the original equations.

Once the points of intersection are found, the slope of the line passing through these points can be determined using the formula:

Slope=
`(Change in y)/(Change in x)`

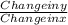
After calculating the slope, the correct answer is found to be -2. This negative slope indicates that the line has a downward inclination. Therefore, the final answer is d. -2.