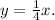Question

What is the equation of the following line passing through the points (8,2) and (0,0)?

a) y = 2x
b) y = -x
c) y = -2x
d) y = x

Answer 1

The equation of the line passing through (8, 2) and (0, 0) is
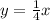`\(y = (1)/(4)x\)`. None of the provided options (a, b, c, d) match the correct equation.

To find the equation of the line passing through the points (8, 2) and (0, 0), you can use the slope-intercept form of the equation
`\(y = mx + b\),`where
`\(m\)` is the slope and
`\(b\)`is the y-intercept.

The slope
`(\(m\))` is given by the change in y divided by the change in x between the two points:

`\[m = \frac{{\text{{change in }} y}}{{\text{{change in }} x}} = \frac{{2 - 0}}{{8 - 0}} = (1)/(4)\]`

Now that we have the slope
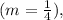`(\(m = (1)/(4)\)),` we can use one of the points to find the y-intercept (\(b\)). Let's use the point (0, 0):

`\[0 = (1)/(4)(0) + b \implies b = 0\]`

Now, we have the slope
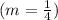`(\(m = (1)/(4)\))` and the y-intercept
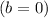`(\(b = 0\))`, so the equation of the line is:

`\[y = (1)/(4)x\]`

Among the given options:

a)
`\(y = 2x\)`(not the correct equation)

b)
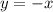`\(y = -x\)`(not the correct equation)

c)
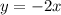`\(y = -2x\)` (not the correct equation)

d)
`\(y = x\)` (not the correct equation)

None of the given options match the correct equation
`\(y = (1)/(4)x\).`