Final answer:
Horizontal dilation by 0.5, vertical dilation by 3, reflection over the x-axis transformations of the graph of f(x) = 3ˣ result in the graph of f(x) = 3 ⋅ 3⁻²ˣ Therefore, correct answer is b) Horizontal dilation by 0.5, vertical dilation by 3, reflection over the x-axis
Step-by-step explanation:
To transform the graph of
 we need to apply a horizontal dilation by 0.5, a vertical dilation by 3, and a reflection over the x-axis. The horizontal dilation by 0.5 is represented by the exponent -2x, the vertical dilation by 3 is due to the coefficient 3 in front of the exponential term, and the reflection over the x-axis is indicated by the negation of the exponent in
we need to apply a horizontal dilation by 0.5, a vertical dilation by 3, and a reflection over the x-axis. The horizontal dilation by 0.5 is represented by the exponent -2x, the vertical dilation by 3 is due to the coefficient 3 in front of the exponential term, and the reflection over the x-axis is indicated by the negation of the exponent in
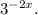
Understanding how different transformations affect the graphs of exponential functions is crucial in mathematics. These transformations, including dilations and reflections, play a significant role in manipulating functions to fit specific requirements or to model various real-world scenarios.
Therefore, correct answer is b) Horizontal dilation by 0.5, vertical dilation by 3, reflection over the x-axis