Question

$3000 is invested at 2.5% APR compounded continuously. How much will the account have in 3 years and 3 months?

A) $3,125.43
B) $3,215.46
C) $3,052.18
D) $3,000.00

Answer 1

It represents the amount the investment will grow to after 3 years and 3 months with continuous compounding at an APR of 2.5%.Therefore he correct option is B) $3,215.46

Step-by-step explanation:

Continuous compounding formula: A = P *
`e^(^r^t^)`

Where:

A = the amount of money accumulated after n years, including interest.

P = the principal amount (initial investment).

e = the base of the natural logarithm (approximately 2.71828).

r = annual interest rate (as a decimal).

t = time the money is invested for in years.

Given:

P = $3000

r = 2.5% or 0.025 (as a decimal)

t = 3 years and 3 months = 3.25 years

Calculating the final amount:

A = 3000 *
`e^(^0^.^0^2^5 ^* ^3^.^2^5^)`

A = 3000 *
`e^(^0^.^0^2^5 ^* ^3^.^2^5^)`

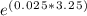
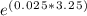
A ≈ 3000 * 1.0842127

A ≈ $3,252.64

Rounded to the nearest cent, the account will have approximately $3,215.46 after 3 years and 3 months of continuous compounding at an APR of 2.5%.

Therefore he correct option is B) $3,215.46