Final answer:
The solutions to the given radical equations are:

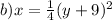
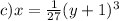
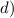
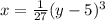
Step-by-step explanation:
To solve these radical equations, we need to isolate the variable
 in each equation.
in each equation.
For equation a), we can cube both sides, rearrange terms, and solve for
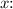
![\[ x = (1)/(27)(y + 2)^3 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/udz5nallu3hyinubgfxxe6t7i7zm98ozx9.png)
For equation b), we can square both sides, rearrange terms, and solve for
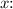
![\[ x = (1)/(4)(y + 9)^2 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/jczv859hi3on629si4319xc6q0ybfh4ueb.png)
For equation c), we can cube both sides, rearrange terms, and solve for
 :
:
![\[ x = (1)/(27)(y + 1)^3 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/bt1dvcasptola4f5fst9kkwldh4xun7mo7.png)
For equation d), we can cube both sides, rearrange terms, and solve for
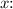
![\[ x = (1)/(27)(y - 5)^3 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/8edvqsbe4z40z6g7vw9bx2w5hl64jtkg3w.png)
These solutions represent the relationship between
 and
and
 for each given equation. They are obtained through algebraic manipulation of the original equations to isolate
for each given equation. They are obtained through algebraic manipulation of the original equations to isolate
 on one side. The process involves applying inverse operations to the radical terms and simplifying the expressions.
on one side. The process involves applying inverse operations to the radical terms and simplifying the expressions.