Question

I am not sure how to use te FTC Part 1 for any of them, how do I show my work?

Answer 1

1. The derivative of the function
`(d)/(dx) \int\limits^x_4 {(ds)/(√(4-s^2) ) } \,` is
`1/\sqrt{(4-x^2).`

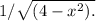
2. The derivative of the function
`(d)/(dx) \int\limits^3_x {(t^5+cos t)} \,dt` is
`-(3^5 + cos(3)).`

3. The derivative of the function
`(d)/(dx) \int\limits^(2x)_1 {(t^2)/(t^2+4) } \,dt` is
`(2x^2 + 4)/(x^2 + 4).`

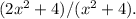
To find the derivative of the first integral, we can apply the Fundamental Theorem of Calculus Part 1.

Using this theorem, we differentiate the expression inside the integral and then multiply it by the derivative of the upper limit of integration, which is x.

In this case, the derivative is 1, so we get the derivative as
`1/\sqrt{(4-x^2).`

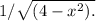
For the second integral, we can again use the Fundamental Theorem of Calculus Part 1.

We differentiate the expression inside the integral with respect to t, and then multiply it by the derivative of the lower limit of integration, which is -1. This gives us the derivative as
`-(3^5 + cos(3)).`

Similarly, for the third integral, we differentiate the expression inside the integral with respect to t, and multiply it by the derivative of the upper limit of integration, which is 2x.

The derivative is then
`(2x^2 + 4)/(x^2 + 4).`

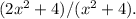
The probable question may be:

Use the FTC Part 1 to find each derivative

1. \frac{d}{dx} \int\limits^x_4 {\frac{ds}{\sqrt{4-s^2} } } \,

2. \frac{d}{dx} \int\limits^3_x {(t^5+cos t)} \,dt

3. \frac{d}{dx} \int\limits^{2x}_1 {\frac{t^2}{t^2+4} } \,dt