Question

I am not sure how to use the FTC Part 1 for any of these three problems can I please have some help on them thank you!

Answer 1

1.
`\[ (d)/(dx) \int\limits_4^x (ds)/(√(4-s^2)) \].` the derivative is
`(1)/(√(4-x^2))`

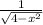
2.
`\[ (d)/(dx) \int\limits_x^3 (t^5 + \cos(t)) \, dt \]` the derivative is
`-(x^5 + \cos(x)) \].`

3.
`\[ (d)/(dx) \int\limits_(2x)^1 (t^2)/(t^2 + 4) \, dt \]` the derivative is
`-((2x)^2)/((2x)^2 + 4) \].\\`

Certainly! Let's solve each of the given problems using the Fundamental Theorem of Calculus Part 1 (FTC Part 1).

1. Problem:

`\[ (d)/(dx) \int\limits_4^x (ds)/(√(4-s^2)) \]`

Solution:

Let
`\( F(t) = \int\limits_4^t (ds)/(√(4-s^2)) \).`

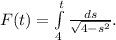
According to FTC Part 1,
`\( (d)/(dx) \int\limits_a^x f(t) \, dt = f(x) \)`, where \( a \) is a constant.

Therefore,

`\[ (d)/(dx) \int\limits_4^x (ds)/(√(4-s^2)) = (1)/(√(4-x^2)) \].`

2. Problem:

`\[ (d)/(dx) \int\limits_x^3 (t^5 + \cos(t)) \, dt \]`

Solution:

Let
`\( G(t) = \int\limits_t^3 (u^5 + \cos(u)) \, du \).`

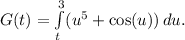
According to FTC Part 1,
`\( (d)/(dx) \int\limits_a^x f(t) \, dt = -f(x) \),`where \( a \) is a constant.

Therefore,

`\[ (d)/(dx) \int\limits_x^3 (t^5 + \cos(t)) \, dt`=
`-(x^5 + \cos(x)) \].`

3. Problem:

`\[ (d)/(dx) \int\limits_(2x)^1 (t^2)/(t^2 + 4) \, dt \]`

Solution:

Let
`\( H(t) = \int\limits_(2t)^1 (u^2)/(u^2 + 4) \, du \).`

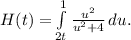
By FTC Part 1,

`\[ (d)/(dx) \int\limits_(2x)^1 (t^2)/(t^2 + 4) \, dt =`
`-((2x)^2)/((2x)^2 + 4) \].\\`

These derivatives are calculated using the FTC Part 1 and are based on the fundamental properties of definite integrals and their connections to derivatives.

The probable question may be:

use the FTC Part 1 to find each derivative

d/dx\int\limits^x_4 {\frac{ds}{\sqrt{4-s^2} } }

d/dx\int\limits^3_x ({t^5+cost }) dt

d/dx\int\limits^2x_1 {\frac{t^2}{t^2+4 } }dt