Question

What is a point-slope equation of the line with slope –10 that goes through the point (1, 4)?

A.y – 4 = –10(x – 1)
B.y + 4 = –10(x + 1)
C.y + 4 = 10(x + 1)
D.y – 4 = 10(x – 1)

Answer 1

The point-slope equation of the line with a slope of -10 that passes through the point (1, 4) is given by option (A) (y - 4 = -10(x - 1). Thus the correct option is A.

Step-by-step explanation:

The point-slope form of a linear equation is
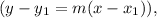`(y - y_1 = m(x - x_1)),` where m is the slope, and
`\((x_1, y_1)\)` is a point on the line. In this case, the slope (m) is given as -10, and the point 1, 4 lies on the line.

Substituting these values into the point-slope formula, we get (y - 4 = -10(x - 1). Now, let's simplify this equation:

[y - 4 = -10x + 10]

To isolate (y), we add 4 to both sides:

[y = -10x + 14]

So, the equation in slope-intercept form is (y = -10x + 14), which is equivalent to the point-slope form (y - 4 = -10(x - 1)). Therefore, option (A) is the correct choice.

In conclusion, option (A) accurately represents the point-slope equation of the line with a slope of -10 that passes through the point (1, 4).