Question

Which expressions are equivalent to (x + 4/3) divided by (6/x)?

Answer 1

Equivalent expressions for (x + 4/3) divided by (6/x) are obtained by multiplying (x + 4/3) by the reciprocal of (6/x), which is (x/6). Distributing this across the terms results in (x^2/6) + (2x/9) in simplified form.

Step-by-step explanation:

To find equivalent expressions for the given expression
`(x + (4)/(3)) / ((6)/(x))`, we can apply the concept that dividing by a number is the same as multiplying by its reciprocal. Therefore, dividing by
`(6)/(x)` is the same as multiplying by the reciprocal of this fraction, which is
`(x)/(6)`.

Now, we re-write the original expression using multiplication by the reciprocal:

`(x + (4)/(3)) * (x)/(6)`

At this point, we can distribute
`(x)/(6)`across the terms inside the parentheses:

`(x^2)/(6) + (4)/(3) * (x)/(6)`

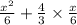
To simplify further, multiply the fractions in the second term by finding a common denominator and combining the numerators, resulting in:

`(x^2)/(6) + (4x)/(18)`

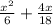
We can simplify the second fraction by dividing both numerator and denominator by 2:

`(x^2)/(6) + (2x)/(9) -`This is the equivalent expression in its simplified form.