Question

Solve for \( \sin(2x) = \text{blank} \)

A. \(1 - 2\sin^2 x\)

B. \(2\sin x \cos x\)

C. \(\frac{1}{2}(\cos(a-b)-\cos(a+b))\)

D. \(2\sin x + 2\cos x\)

Answer 1

The solution is
`\(2\sin x \cos x\)`, derived from the double-angle identity for sine
`(\( \sin(2x) = 2\sin x \cos x\))`. This matches option B, making it the correct choice. The B is correct option.

Step-by-step explanation:

The given trigonometric equation is
`\( \sin(2x) \)` and we need to express it in terms of known trigonometric functions. Utilizing the double-angle identity for sine,
`\( \sin(2x) = 2\sin x \cos x \)`, we can observe that this matches option B. Therefore, the correct answer is B.

Now, let's delve into the explanation. The double-angle identity for sine is
`\( \sin(2x) = 2\sin x \cos x \)`, a fundamental trigonometric relationship. To understand this identity, consider the angle
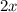`\(2x\)` as the sum of two angles
`\(x\)` and
`\(x\)`. The identity reveals a connection between the sine of
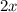`\(2x\)` and the product of sine and cosine of
`\(x\)`. This relationship is vital in simplifying expressions involving trigonometric functions.

In option A,
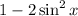`\(1 - 2\sin^2 x\)`, this is an application of the double-angle identity for cosine
`(\( \cos(2x) = 1 - 2\sin^2 x \))`, not for sine. Option C introduces the sum and difference identities for cosine, which are not directly related to the given equation. Option D combines sine and cosine but lacks the double-angle form present in the original equation. By recognizing and applying the appropriate trigonometric identity, we arrive at the correct solution:
`\(2\sin x \cos x\)`, as stated in option B. Therefore option B is correct.