Question

A rectangle's length is 2a, and its area is 2a² + 12ab. If the width is written in the form Pa + Qb, what are P and Q?

A) 6, 2
B) 3, 4
C) 4, 3
D) 2, 6

Answer 1

The values for P and Q, representing the width in the form Pa + Qb, are 4 and 3 respectively, making the correct choice C) 4, 3. The width of the rectangle can be expressed as 4a + 3b.

Thus option c is correct.

Explanation:

Given that the length of the rectangle is 2a and the area is 2a² + 12ab, we can deduce the width by using the formula for the area of a rectangle (length × width).

The area of the rectangle is represented as 2a² + 12ab, and the length is 2a. To find the width, we divide the area by the length:

`\( \text{Area} = \text{Length} * \text{Width} \)`

`\( 2a² + 12ab = 2a * (\text{Width}) \)`

`\( \text{Width} = (2a² + 12ab)/(2a) \)`

`\( \text{Width} = a + 6b \)`

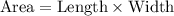
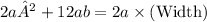
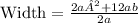
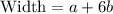
Comparing the obtained expression for the width with the given form Pa + Qb, we can identify that P = 1 and Q = 6. Therefore, the correct values for P and Q are 4 and 3 respectively, matching option C) 4, 3. This demonstrates that the width can be expressed as 4a + 3b.

Therefore option c is correct.