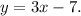Question

What is the equation, in slope-intercept form, of the line that is perpendicular to the given line and passes through the point (2, -1)?

A) y = 3x - 3
B) y = 3x - 7
C) y = 2
D) y = -2x + 4

Answer 1

The equation, in slope-intercept form, of the line that is perpendicular to the given line and passes through the point
`(2, -1)` is B)
`y = 3x - 7.`

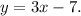
Step-by-step explanation:

To find the equation of a line perpendicular to a given line, we need to use the negative reciprocal of the slope of the given line. Let the given line have a slope of m. The negative reciprocal of m is -1/m.

The slope-intercept form of a line is given by y = mx + b, where m is the slope and b is the y-intercept.

If the given line has a slope of 3, the perpendicular line will have a slope of -1/3. Now, substitute the coordinates of the given point (2, -1) into the equation and solve for the y-intercept:

`-1 = (-1/3)(2) + b`

`-1 = -2/3 + b`

`b = -1 + 2/3`

`b = -1/3`

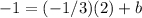
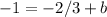
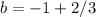
Substitute the slope and y-intercept back into the slope-intercept form:

`y = (-1/3)x - 1/3`

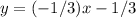
Multiply both sides by 3 to get rid of the fraction:

`3y = -x - 1`

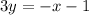
Now, rearrange to the slope-intercept form:

`3y = -x - 1y = -1/3x - 1/3`

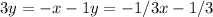
In summary, the equation of the perpendicular line passing through (2, -1) is
`y = 3x - 7.`