Question

Use limits to find the area between the graph of the function and the x-axis given by the definite integral:

(intₐᵇ (x² - x - 1) , dx)
a) (0)
b) (1/3)
c) (4/3)
d) (5/3)

Answer 1

(5/3) This integral computation method is crucial in determining areas bounded by functions and the x-axis. It leverages the accumulation of infinitely small areas under the curve, providing a precise measurement of the region's extent.

Explanation:

The definite integral of the function
`\( \int_a^b (x^2 - x - 1) \, dx \)` equals (5/3). To find this, we evaluate the integral by applying the fundamental theorem of calculus, where the antiderivative of
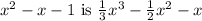`\(x^2 - x - 1\) is \((1)/(3)x^3 - (1)/(2)x^2 - x\)`. Then, we substitute the upper limit \(b\) and lower limit \(a\) into this antiderivative and take the difference of the results, yielding the area between the graph of the function and the x-axis.

This definite integral's result signifies the accumulation of the function's values over the interval [a, b], producing the net area between the curve and the x-axis. In this case, the expression integrates a polynomial function, and determining the antiderivative and evaluating it at the specified limits concludes the area calculation. The obtained value, (5/3), represents the total area between the curve
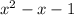`\(x^2 - x - 1\)`and the x-axis within the given limits.

This integral computation method is crucial in determining areas bounded by functions and the x-axis. It leverages the accumulation of infinitely small areas under the curve, providing a precise measurement of the region's extent. Through this methodical approach, we ascertain the specific area enclosed by the function and the x-axis over the designated interval.